Analytics Exercise: An MRP Explosion – Brunswick Motors
Instructions:
Complete the “Analytics Exercise: An MRP Explosion – Brunswick Motors,” at the end of Chapter 21 in the textbook. Answer Questions 1-3. (275 words per question)
Jacobs, F. R., Chase, R. B. (2014). Operations and supply chain management (14th ed.). New York, NY: McGraw-Hill. ISBN-13: 9780078024023
Analytics Exercise: An MRP Explosion—Brunswick Motors
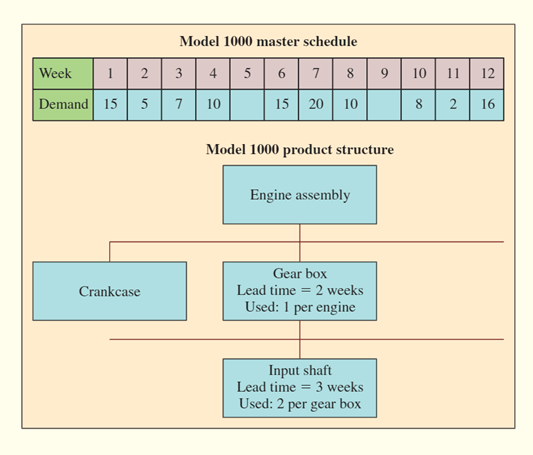
Recently, Phil Harris, the production control manager at Brunswick, read an article on time-phased requirements planning. He was curious about how this technique might work in scheduling Brunswick’s engine assembly operations and decided to prepare an example to illustrate the use of time-phased requirements planning. Phil’s first step was to prepare a master schedule for one of the engine types produced by Brunswick: the Model 1000 engine. This schedule indicates the number of units of the Model 1000 engine to be assembled each week during the last 12 weeks and is shown below. Next, Phil decided to simplify his requirements planning example by considering only two of the many components that are needed to complete the assembly of the Model 1000 engine. These two components, the gear box and the input shaft, are shown in the product structure diagram below. Phil noted that the gear box is assembled by the Subassembly Department and subsequently is sent to the main engine assembly line. The input shaft is one of several component parts manufactured by Brunswick that are needed to produce a gear box subassembly. Thus, levels 0, 1, and 2 are included in the product structure diagram to indicate the three manufacturing stages that are involved in producing an engine: the Engine Assembly Department, the Subassembly Department, and the Machine Shop. The manufacturing lead times required to produce the gear box and input shaft components are also indicated in the product structure diagram. Note that two weeks are required to pro-duce a batch of gear boxes and that all the gear boxes must be delivered to the assembly line parts stockroom before Monday morning of the week in which they are to be used. Likewise, it takes three weeks to produce a lot of input shafts, and all the shafts that are needed for the production of gear boxes in a given week must be delivered to the Subassembly Department stockroom before Monday morning of that week. In preparing the MRP example Phil planned to use the worksheets shown on the next page and to make the following assumptions:
1. Seventeen gear boxes are on hand at the beginning of Week 1, and fi ve gear boxes are currently on order to be delivered at the start of Week 2.
2. Forty input shafts are on hand at the start of Week 1, and 22 are scheduled for delivery at the beginning of Week 2.
Questions
- Initially, assume that Phil wants to minimize his inventory requirements. Assume that each order will be only for what is required for a single period. Using the following forms, calculate the net requirements and planned order releases for the gear boxes and input shafts. Assume that lot sizing is done using lot-for-lot (L4L).
- Phil would like to consider the costs that his accountants are currently using for inventory carrying and setup for the gear boxes and input shafts. These costs are as follows:

Given the cost structure, evaluate the cost of the schedule from question 1. Assume inventory is valued at the end of each week.
3. Find a better schedule by reducing the number of orders and carrying some inventory. What are the savings with this new schedule?
Solution
Analytics Exercise: An MRP Explosion – Brunswick Motors
From the case of Brunswick motors, a hierarchical composition product structure listing raw materials, assembly methods, parts, and quantities of an engine assembly process is given. From the model, it is indicated that an engine assembly requires a gearbox and can be assembled within a week. Each gear box each of the gear boxes assembled by the company are fitted with two input shafts that require a lead time of three weeks to assemble. The master engine assembly schedule indicates a twelve-week assembly schedule alongside the quantities produced weekly.
Question 1: Initially, assume that Phil wants to minimize his inventory requirements. Assume that each order will be only for what is required for a single period. Using the following forms, calculate the net requirements and planned order releases for the gear boxes and input shafts. Assume that lot sizing is done using lot-for-lot (L4L)
Based on the engine assembly master schedule and the general product structure, one gear box is required for every engine assembled. It is important to consider the engine requirements as stipulated in the master schedule before any other information. After acquiring the information required, any other knowledge from the production process is considered. It is important to note that there are other seventeen gear boxes on site at the beginning of the production (Cafferky & Wentworth, 2010). According to Jacobs & Chase (2014), L4L is a discrete order quantity method where the net requirements of each period represent the quantity of the order. Based on the information provided the net requirements for the planned order release shall be tabulated as follows;
Table 1; engine assembly master schedule
| Weeks | PD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Quantity produced | 15 | 5 | 7 | 10 | 15 | 20 | 10 | |
According to the information from the engine assembly master schedule in the table 1 above the lot size
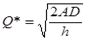
where Q is the lot size, A is the constant set to produce a purchase lot, D is the demand rate, and h is the holding cost, after the first round of production for the gear box shall be as in table2. This is done considering that production is instantaneous, the delivery is immediate, the demand is deterministic and constant over time, there is a constant setup cost in the production, and the products can be analyzed (Omar & Supadi, 2003).
Table 2; gear box
| Weeks | PD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Gross requirement | 15 | 5 | 7 | 10 | 15 | 20 | 10 | 8 | 2 | 16 | |||
| Scheduled receipt | 5 | ||||||||||||
| Projected available balance | 17 | 2 | 2 | ||||||||||
| Net requirements | 5 | 10 | 15 | 20 | 10 | 8 | 2 | 16 | |||||
| Planned order receipts | 5 | 10 | 15 | 20 | 10 | 8 | 2 | 16 | |||||
| Planned order releases | 5 | 10 | 15 | 20 | 10 | 8 | 2 | 16 |
For every gear box produced there are two shafts that are assembled in it each with a lead time of three weeks. This results into;
| Weeks | PD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Gross requirement | 10 | 20 | 30 | 40 | 20 | 16 | 4 | 32 | |||||
| Scheduled receipt | 22 | ||||||||||||
| Projected available balance | 40 | 30 | 32 | 2 | |||||||||
| Net requirements | 38 | 20 | 16 | 4 | 32 | ||||||||
| Planned order receipts | 38 | 20 | 16 | 4 | 32 | ||||||||
| Planned order releases | 38 | 20 | 16 | 4 | 32 |
Question 2: Phil would like to consider the costs that his accountants are currently using for inventory carrying and setup for the gear boxes and input shafts. These costs are as follows:
Part Cost
Gear box setup = $90 / order
Inventory carrying cost = $2 / unit /week
Input shaft setup = $ 45/ order
Inventory carrying cost = $ 1/ unit/ week
Given the cost structure stipulated in question 1, the cost of the entire schedule when the inventory is valued at the end of every week shall be;
Inventory = ending inventory x holding cost
4 x 2 = $8
Setup Cost = total inventories x setup
8 x 90 = $720
Gear Box cost = setup cost + inventory
Total = $720 + $ 8 =$728
Inventory = total ending inventory x holding cost
96 x 1 = $96
Setup Cost = planned inventories x setup
5 x 45 = $225
Input Shaft = setup cost + inventory
Total = $225 + $96 = $321
The total cost for the gear box and the input shaft = gear box cost + input shaft cost
Total Cost = $728 + $321 = $1,049
Question 3: Find a better schedule by reducing the number of orders and carrying some inventory. What are the savings with this new schedule?
To derive a better and cost effective method of production the Least total cost method (LTC) will be used. The LTC is a dynamic sizing technique used lot sizing to calculate the order quantity (Cafferky & Wentworth, 2010). The method compares the carrying cost to the setup cost based on the different lot sizes before selecting the lot in which the two are almost equal or equal (Jacobs & Chase, 2014). This shall result into;
| Engine Assembly Master schedule | |||||||||||||
| Weeks | PD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Quantity produced | 15 | 5 | 7 | 10 | 15 | 20 | 10 | 8 | 2 | 16 |
| Gear box requirements | |||||||||||||
| Weeks | PD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Gross requirement | 15 | 5 | 7 | 10 | 15 | 20 | 10 | 8 | 2 | 16 | |||
| Scheduled receipt | 5 | 26 | |||||||||||
| Projected available balance | 2 | 2 | 10 | 30 | 10 | 18 | 16 | ||||||
| Net requirements | 5 | 10 | 45 | 20 | 10 | 8 | 2 | 16 | |||||
| Planned order releases | 15 | 10 | 45 | 15 | 26 | 2 |
| Input shaft requirements | |||||||||||||
| Weeks | PD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Gross requirement | 30 | 90 | 52 | ||||||||||
| Scheduled receipt | 22 | ||||||||||||
| Projected available balance | 10 | 32 | 32 | ||||||||||
| Net requirements | 58 | 52 | |||||||||||
| Planned order releases | 58 | 52 |
Based on the new figures;
Inventory = ending inventory x holding cost
88x 2 = $176
Setup Cost = total inventories x setup
3 x 90 = $270
Gear Box cost = setup cost + inventory
Total = $270 + $ 176 =$446
Inventory = total ending inventory x holding cost
74 x 1 = $74
Setup Cost = planned inventories x setup
2 x 45 = $90
Input Shaft = setup cost + inventory
Total = $90 + $74 = $164
The total cost for the gear box and the input shaft = gear box cost + input shaft cost
Total Cost = $446 + $164 = $610
Total savings using the Least total cost method over L4L is $439.
References
Cafferky, M. & Wentworth, J. (2010) Breakeven analysis: the definitive guide to cost-volume-
Profit analysis, 2nd ed. New York, NY, Business Expert Press.
Jacobs, R., & Chase, B. (2014). Operations and supply chain management, 14th ed. New York,
NY, McGraw-Hill Publishers.
Omar, M. & Supadi, S. (2003). A Lot-for-Lot model with multiple instalments for a production
system under time-varying demand process. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.581.4444&rep=rep1&type=pdf

