Inventory management
Question 1
Dee Rodgers and Carol Millican own a start-up company which just began supplying the JoPro mini-cam. Both Dee and Carol expect to sell 900 cams over the next year (300 days), but they are uncertain as to how they should procure and inventory the cameras.
Dee prefers to order the cameras from an outside supplier where she can obtain them at $50.00 a camera to be delivered within 2 days of an order. She estimates ordering cost at $20.00/order. Annual carrying charges include 15% interest charge along with insurance and taxes that amount to $2.50 per unit of average inventory (these are two separate costs and both need to be factored into Ch).
Carol prefers to produce the cameras internally. She claims that the company has current capacity to produce 6 cameras a day. The setup cost (ordering) and carrying costs remain the same as if the cameras were purchased from an external vendor.
- If Dee’s plan is followed, how many cameras should they order at one time, what is the reorder point, and what is the associated total annual inventory cost? Support your solution with calculations.
- If Carol’s plan is followed, how many cameras should they produce at one time, what is the time between the start of consecutive production runs, and what is the associated total annual inventory cost? Support your solution with calculations
- Which plan would you recommend and why?
- Suppose Dee finds a dealer that will give her a 2% discount on her original unit cost in part (a) if she orders at least 900 cases at a time. (Assume ordering cost remains at $20/order). Would your recommendation change? Explain why or why not
- Suppose that Dee wants to investigate the possibility of backordering cameras. She estimates that the stockout cost would be only $.50 per camera per year. For this plan, how many cameras should be ordered at one time, what is the reorder point, and what is the associated total annual inventory cost?
- What is your final suggestion to Dee and Carol concerning the inventory policy that they should adopt? Why?
Illustrate each of the above inventory policies with the appropriate diagrams.
Question 2
A product has the following bill of materials:
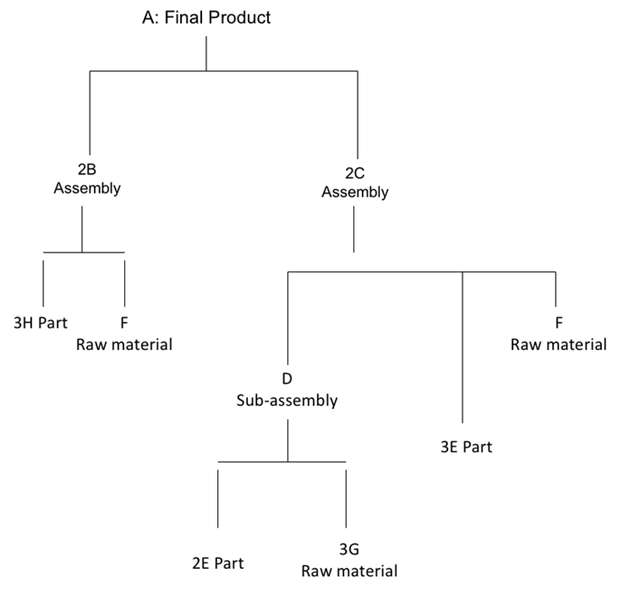
You also have the following information:
| Item | On Hand | Time to Produce | Receipts: Scheduled Quantity | To be received in week |
| A | 500 | 1 | 1000 | 1 |
| B | 1000 | 1 | 1000 | 2 |
| C | 1000 | 1 | ||
| D | 300 | 1 | ||
| E | 500 | 1 | ||
| F | 2000 | 3 | ||
| G | 400 | 2 | 6000 | 1 |
| H | 2500 | 2 | 4000 | 2 |
Prepare an MRP schedule for all of the components in the product to cover an 8-week planning horizon
Solution.
Inventory management
- If Dee’s plan is followed, how many cameras should they order at one time, what is the reorder point, and what is the associated total annual inventory cost? Support your solution with calculations.
The economic order quantity according to Dee’s plan shall be calculated using the formulae;
Economic order quantity = square root of [(2 x demand x ordering costs) ÷ carrying costs]
This is shown as follows
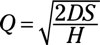
Where Q denotes the economic order quantity, D is annual demand in units; S is the ordering costs while H is the carrying cost per unit.
Q= Economic order quantity = square root of [(2 x demand x ordering costs) ÷ carrying costs]
Q= √ (2*900*20)/2.5
Q= √36,000/2.5
Q=√14,400
Q=120 Cameras
- What is the reorder point?
For the reorder point, we shall multiply the average daily usage for the cameras by the lead time it takes after a replenishment order is made;
Thus,
Reorder point= Average daily sales* lead time
Average daily sales = Total annual sales /300days
Average daily sales = 900/300
Average daily sales = 3
Lead time = 2 days
Re order point= average daily sales * lead time
Re order point= 3*2
Reorder point= 6 cameras
- Total inventory costs
Using the formula
TIC = C (Q/2) + F (D/Q) Where, C=Carrying cost per unit per year Q=Quantity of each order F=Fixed cost per order D=Demand in units per year.
Substituting our values into this formula, we obtain;
TIC = 2.5(120/2) +20(900/120)
TIC= (150) + (150)
TIC= $300
Therefore, the company will incur a total inventory cost of $300 for the year which includes both ordering and holding costs.
2) If Carol’s plan is followed, how many cameras should they produce at one time, what is the time between the start of consecutive production runs, and what is the associated total annual inventory cost? Support your solution with calculations
Modifying the EOQ formulae to consider the in-house production of the cameras, we use the formula:
- EPQ= √ ((2* D*Co*P)/ (Ci*(P-D)))
Where EPQ is the economic production quantity;
D = Annual demand for the product
P = Annual rate of production
Co= fixed cost per setup or the setup cost
Ci= Inventory holding cost per unit
EPQ= √ ((2*900*20*(6*300))/(2.5*(1800-900)
EPQ= √ ((64,800,000/2250))
EPQ= √ ((28800
EPQ=170
ii) Time between production runs
This is the time lapse between one productions run to the other. We shall use the formula
= (EPQ/ D) * Number of working days in a year
=(170/900)*300
= 57 days
iii) Annual inventory costs
In order to calculate the annual inventory costs, we shall use the formula below;
TIC = C (Q/2) + F (D/Q) Where, C=Carrying cost per unit per year Q=Quantity of each order F=Fixed cost per order D=Demand in units per year. Substituting our values into the formula, we obtain;
TIC=2.5(170/2)+ 20(900/170)
TIC= 2.5(85)+ 20(5.294)
TIC= 212.5+105.88
TIC= $318.38
- Recommendation
3. Based on the above calculations, the company is better off purchasing the cameras from third parties as it reduces the inventory costs by approximately $18.38.
4. Suppose Dee finds a dealer that will give her a 2% discount on her original unit cost in part (a) if she orders at least 900 cases at a time. (Assume ordering cost remains at $20/order). Would your recommendation change? Explain why or why not
i) In order to answer this question, we first establish the savings that the company would realize if they took the discount.
Savings from the new purchase =2%*50*900
= 0.02*50*900
= $900
We also calculate the incremental total costs resulting from the additional carrying costs as a result of the larger order.
TIC = C (Q/2) + F (D/Q) Where, C=Carrying cost per unit per year Q=Quantity of each order F=Fixed cost per order D=Demand in units per year.
=2.5(900/2)+20 (900/900)
=2.5(450)+20
=1125+20
=$1,145
Incremental inventory costs = New inventory cost – original inventory costs
Incremental costs= $1,145- $300
Incremental costs =845
- Since the company gets a discount of $900 against an incremental carrying cost of $845, it’s recommended that the company should accept to order 900 units at the new discount since there is a net gain of $900-$845 = $55
In this case, it would be recommended that the company adopts Dee’s proposal with the 2% discount since it results in a net positive saving.
5. Suppose that Dee wants to investigate the possibility of backordering cameras. She estimates that the stock out cost would be only $.50 per camera per year. For this plan, how many cameras should be ordered at one time, what is the reorder point, and what is the associated total annual inventory cost?
- Q=√(2*P*D)/h * (S+h)/S
Where P is the price per camera, D is the annual demand, h is the holding cost per camera, and S is the stock out cost per camera.
Substituting this to our formula, we obtain,
Q= √((2(50*900)/2.5))(0.5+2.5)/0.5
Q=√((90000/2.5)(3/0.5)
Q=√(36,000*6
Q= √216000
Q=465
6. Recommendation
From the above calculations, it’s evident that the company would save more if they make a onetime order of 900 cameras at a 2% discount as it will result in significant net savings for the company.
QUESTION 2
Material Requirements Plan
| A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=1 | 3000 | 4500 | ||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 3000 | 4500 |
| Scheduled Receipts | 1000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 500 | 1500 | 1500 | 1500 | 1500 | 1500 | 1500 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 1500 | 4500 |
| Planned order releases | 0 | 0 | 0 | 0 | 0 | 1500 | 4500 | 0 |
| B | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=1 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 6000 | 9000 |
| Scheduled Receipts | 0 | 1000 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 1000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 4000 | 9000 |
| Planned order releases | 0 | 0 | 0 | 0 | 0 | 4000 | 9000 | 0 |
| C | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=1 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 6000 | 9000 |
| Scheduled Receipts | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 0 |
| Planned receipts | 5000 | 9000 | ||||||
| Planned order releases | 0 | 0 | 0 | 0 | 0 | 5000 | 9000 | 0 |
| D | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=1 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 3000 | 4500 |
| Scheduled Receipts | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 2700 | 4500 |
| Planned order releases | 0 | 0 | 0 | 0 | 0 | 2700 | 4500 | 0 |
| E | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=1 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 15000 | 22500 |
| Scheduled Receipts | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 500 | 500 | 500 | 500 | 500 | 500 | 500 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 14500 | 22500 |
| Planned order releases | 0 | 0 | 0 | 0 | 0 | 14500 | 22500 | 0 |
| F | 1 | 2 | 3 | ` | 5 | 6 | 7 | 8 |
| L4L,L=3 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 6000 | 9000 |
| Scheduled Receipts | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 4000 | 4500 |
| Planned order releases | 0 | 0 | 0 | 1000 | 4500 | 0 | 0 | 0 |
| G | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=2 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 9000 | 13500 |
| Scheduled Receipts | 6000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 400 | 6400 | 6400 | 6400 | 6400 | 6400 | 6400 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 2600 | 13500 |
| Planned order releases | 0 | 0 | 0 | 0 | 2600 | 13500 | 0 | 0 |
| H | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| L4L,L=2 | ||||||||
| Gross Requirements | 0 | 0 | 0 | 0 | 0 | 0 | 9000 | 13500 |
| Scheduled Receipts | 0 | 4000 | 0 | 0 | 0 | 0 | 0 | 0 |
| Projected on hand inventory | 2500 | 6900 | 6900 | 6900 | 6900 | 6900 | 6900 | 0 |
| Planned receipts | 0 | 0 | 0 | 0 | 0 | 0 | 2100 | 13500 |
| Planned order releases | 0 | 0 | 0 | 0 | 2100 | 13500 | 0 | 0 |
References
Guga,E & Musa,O. (2015) Inventory Management Through EOQ Model A Case Study Of Shpresa Ltd, Albania. International Journal of Economics, Commerce and Management. Retrieved from: http://ijecm.co.uk/

